文:俞欣豪( 認知科學博士,目前是澳洲莫納許大學 (Monash University) 的研究員。專長是靈長類動物的視覺系統。)

source:wikimedia
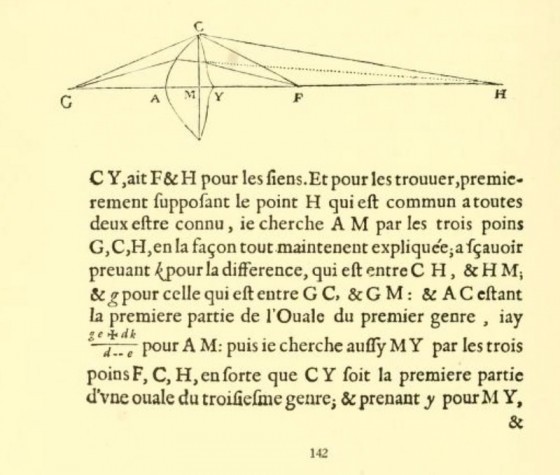
法國哲學家笛卡爾在一六三七年發表了《幾何學》(La Géometrie)。這篇長文是《方法論》的一部份,它首創分析幾何學,是西方文明最重要的著作之一。不過這本書中的一張插圖有錯,一直要等到將近四個世紀後的公元兩千一二年才被發現。奇怪的是發現這個錯誤的人,不是數學家,不是歷史學家,而是研究三葉蟲的古生物學家。
為什麼古生物學家會鑽研笛卡爾?笛卡爾跟三葉蟲到底有什麼關係?
這張有錯誤的圖出現在《幾何學》的第二冊。笛卡爾在這裡解釋如何繪製一種我們今日稱為「笛卡爾橢圓」(Cartesian ovals)的平面曲線。為什麼笛卡爾要大費周章研究這種曲線?這個問題不是很容易解答,連笛卡爾自己都沒有在書裡解釋清楚,我們要稍微瞭解一下笛卡爾的學術生涯才行。
跨足多領域的學術生涯
笛卡爾在一六三七年發表了《方法論》(Discours de la méthode)。他在這本書裡討論如何用理性思維精確地獲得知識。眾所皆知的「我思故我在」,就首次出現於《方法論》的第四講。有些介紹笛卡爾的文章太過於強調《方法論》裡抽象的哲學思維,讓讀者以為笛卡爾用《方法論》當工具,得到最重要的成果,是證明了上帝與自我的存在。其實《方法論》只是導論,笛卡爾在《方法論》後附上三篇長文,用來展示這種思考方式得到的成果。這三篇長文分別是:《氣象學》(Les Météores)、《折光學》(La Dioptrique)、與《幾何學》(La Géométrie),這說明了笛卡爾相信他的方法學,主要的應用是在於自然科學與數學。
笛卡爾的思考是非常深刻而且多樣化的,這三篇長文討論三個看似獨立的主題,其實有許多共同的脈絡。以《折光學》為例,笛卡爾在《折光學》的第二講裡推導出了光波折射,入射角與折射角之間的數學關係[1]。這是一個了不起的成就,因為它是解釋許多自然現象的關鍵。例如《氣象學》就利用這個公式解釋彩虹的形狀。更重要的是在《折光學》裡,笛卡爾把折射定律運用在人體最重要的光學器官 — 眼睛。他解釋了影像是如何投射在視網膜上,推測近視與遠視的成因,並且討論如何用透鏡彌補眼睛構造天生的不足。為了看到肉眼不能看到的東西,笛卡爾分析了放大鏡、望遠鏡、顯微鏡的原理。《折光學》展現出來的務實的笛卡爾,他追隨法蘭西斯·培根等人的論點,致力於發展一種為人類需求服務的知識。
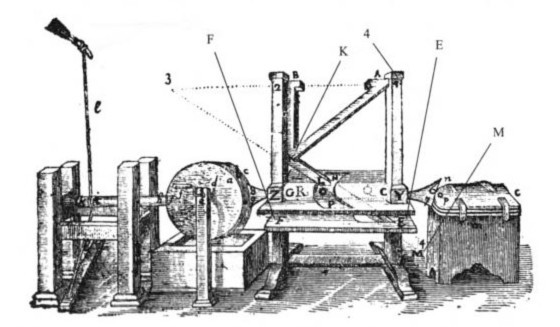
講起務實,笛卡爾可能比大部分人的想像還要務實的多。《折光學》最後一講描述一種機器,在理論上可以自動磨出前所未有的高品質鏡片。事實上在《折光學》發表之前,笛卡爾就已經花了超過十年的時間研發這種機器。在一六二零年代,笛卡爾還住在法國的時候,他就跟工匠合作試圖磨出特殊設計的鏡片。體弱多病,一天到晚躲在房間裡的笛卡爾,甚至在工廠裡親自監工。一六二九年笛卡爾移居荷蘭,不過還是不忘從遠方監督法國工廠的進度。用我們今日的話講,笛卡爾是十七世紀的新創公司創業者。當時的產業界跟今日沒有很大的差別,也是有許多競爭者,有非常高的風險。笛卡爾花了大筆投資人的錢,雖然製造出了一些產品的原型,不過品質達不到期望的標準,最後放棄。在《折光學》的最後一章,笛卡爾乾脆把他的商業機密用開源(open source)的形式提供給歐洲學界,希望有別人能夠完成他的夢想。
透鏡在從中古時代被就用來矯正視力[2],所以磨透鏡在笛卡爾的時代並不是什麼新鮮事。不過十七世紀初,透鏡突然變成了不折不扣的高科技,這是因為伽利略這些科學家開始發展出高倍數望遠鏡。這些新的儀器除了有天文學的應用外,還有軍事價值,立刻就受到各界的注意。
完美的形狀,不完美的透鏡
當時的笛卡爾掌握了這方面的關鍵技術:他推導出來的折射定律,讓他成為最早能用分析性思維,探討透鏡跟視覺關係的人。這跟當時磨鏡片的工匠,用經驗法則行事,有很大的不同。此外,笛卡爾發明了分析幾何學。他把幾何與代數這兩個原來不相關的學問結合起來,發現許多困難的幾何問題,都能迎刃而解。這些發現最後發表在《幾何學》裡。
《幾何學》是數學史上最重要的著作之一,它的主要內容看似非常理論化,是要解決古希臘數學的幾何曲線分類問題,不過笛卡爾也沒有忽略分析幾何在解決實際問題上的威力。《幾何學》第二冊裡有相當的篇幅討論各種橢圓形的畫法,其實那些都是光線在不同介質裡折射問題的解。《幾何學》的這個部分,是在發展設計透鏡的數學工具。
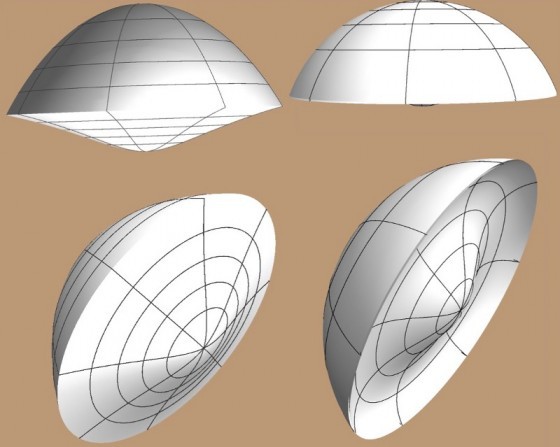
十七世紀使用的光學鏡片,跟我們熟悉的放大鏡類似,都是球面鏡片。也就是說這些鏡片雖然不是球體,不過它們的兩個曲面,都是球面的一小部分。球面鏡片容易磨製,而且希臘人認為球體是完美的形狀,不難理解為什麼用在鏡片上。笛卡爾用他自己發明的數學工具分析成像,發現球面鏡片有重大的缺點,那就是遠方傳來的平行光,在球面鏡片的彎折後,不會聚焦在同一點上,因此造成模糊的影像。這個現象我們今日稱為「球面像差」(spherical aberration)。
笛卡爾推導出非球面鏡片的公式,用來解決球面像差的問題。根據史料,歷史學家相信笛卡爾用手工磨片的方法,製造出了少量的非球面鏡片,但因為精確度的問題,這些鏡片並沒有比一般的球面鏡片優秀。笛卡爾相信他設計的機器可以取代人工,可以大量的產生精確的非球面鏡片,不過理論畢竟跟實際有許多差距,笛卡爾花了十五年的時間跟不同的工匠合作,用盡了創業基金,還是沒有辦法實踐他的自動磨片機。
《折光學》出版後在歐洲的科學界引起了研究非球面鏡片的風潮,許多科學家都加入研發非球面鏡片的行列。例如說在一六九零年荷蘭科學家惠更斯(Christiaan Huygens)發表了《光學理論》(Traité de la Lumière),在這本書裡,他不但描述了光的波動理論,還推導出了跟笛卡爾不一樣的非球面鏡片公式。牛頓也曾經試著研磨非球面鏡片,不過因為牛頓對於光學有更深入的了解,他發現校正球面像差並不能解決所有的光學問題[3],因此非球面鏡片並沒有笛卡爾想像中的完美。非球面鏡片的製成技術因為難度高,久久沒有突破,科學家漸漸把注意力轉移到反射望遠鏡以及其它光學科技上。非球面透鏡的問題,慢慢的被遺忘了。令人欣慰的是實踐笛卡爾構想,的確是有成功的例子。《折光學》發表三十年後的一六六七年,英國科學家 Francis Smethwick 第一次磨出高品質的非球面鏡片,因此製造出非常高效能的望遠鏡,不過他的設計沒有普及化。
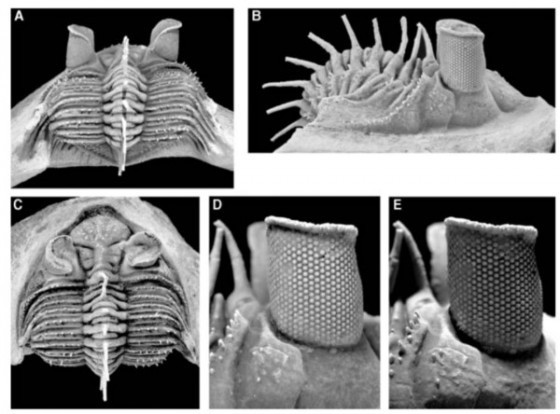
摩洛哥出土的三葉蟲 Erbenochile erbeni 化石。注意它精密的眼睛構造。圖出自 Fortey, R. & Chatterton, B. (2003) A Devonian trilobite with an eyeshade. Science 19, 1689.
由古老三葉蟲發展出新突破
笛卡爾的非球面鏡片沒有普遍化,不過奇怪的是演化這個「盲目的鐘錶匠」[4]居然在冗長的生物演化史中,製造出了非球面鏡片。這就得提起三葉蟲了。三葉蟲最早出現於五億三千萬年前,整整有三億年的時間,是地球上最成功的動物之一。三葉蟲的種類繁多,有超過上萬種物種。一般逛博物館的人對三葉蟲的印象是大型蟑螂。常見的三葉蟲化石,眼睛小而且構造看似原始,多數人大概不會想到有些三葉蟲是靠視覺捕殺獵物的動物。不過有些三葉蟲有非常精細的椱眼構造,吸引了視覺科學家的注意。
視覺科學跟古生物學沒有太大的重疊,那是因為動物眼睛裡的光學元件,如角膜與水晶體,大多是由細胞組成,這種軟組織不會留下化石,因此無法研究。三葉蟲是個例外。它們的複眼裡,折光的元件是生物體合成的方解石,是礦物,因此保留到今日。這是一個讓我們探索古生物的視覺系統的難得機會[5]。一九七五年古生物學家與物理學家合作,開始研究三葉蟲複眼裡透鏡的幾何結構,他們發現有兩個三葉蟲物種,透鏡的形狀跟笛卡爾、惠更斯提出的非球面鏡片,有驚人的相似性,因此推測它們的功能是對抗球面像差,用來增加視覺的感光度。
摩洛哥出土的三葉蟲 Erbenochile erbeni 化石。注意它精密的眼睛構造。圖出自 Fortey, R. & Chatterton, B. (2003) A Devonian trilobite with an eyeshade. Science 19, 1689.
造物者的偏心?
這篇文章討論的主題實在是有點隱晦,古生物學,光學,數學史這些內容,應該是只有學者會有興趣。不過你要是用 Google 搜尋三葉蟲眼睛的資訊,就會發現有些基督教創造論的網站,在講三葉蟲。創造論信徒翻遍了所有科學文獻,不論什麼隱晦的內容,都可以拿來作為反對演化論的依據,連三葉蟲的眼睛構造這麼冷門的主題都不放過。這些文章通常充滿錯誤的科學知識,與邏輯謬誤,不值得在這裡詳細檢討。最重要的地方在他們誤解了笛卡爾非球面鏡片的意義。創造論者說因為三葉蟲的透鏡結構類似笛卡爾用數學推導出來的「完美鏡片」,所以可以推論這種眼睛構造,一定是完美的造物者設計出來的,不可能是演化的結果。
第一個問題是只有少數的三葉蟲物種有這種眼睛,不是所有的三葉蟲都有,因此我們得問為什麼造物者這麼偏心,給別的三葉蟲不完美的眼睛。更重要的問題是是笛卡爾的鏡片,是為了解決特定問題而設計出來的,用在顯微鏡與望遠鏡上,是理論上的最佳解[6],但作為生物的視覺器官,其實不是個好設計。三葉蟲用方解石作為透鏡,不像我們的水晶體可以依照需求改變形狀,是非常嚴重的缺陷,是盲目的演化過程陷入的死路,非球面透鏡是修正這種缺陷不得不演化出來的設計。三葉蟲的視覺系統比早期古生物學家的推測精密,不過跟現代動物比起來仍然是非常的原始,有許多嚴重缺陷,並不是創造論者所說的「完美眼睛」。
有點諷刺的是笛卡爾寫《折光學》,正是因為他分析人類眼睛的光學性質,發現它有許多缺陷。笛卡爾相信理性與科學知識,可以補償天性的不足。如果造物者給我們設計了完美的眼睛,那笛卡爾就不用研究非球面鏡片了。
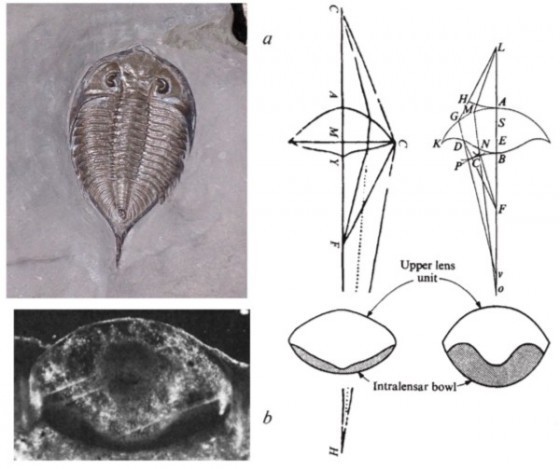
上圖比較三葉蟲物種 Dalmanitina socialis 的透鏡構造,跟笛卡爾《幾何學》裡的插圖的相似性。有個令人擔心的地方,是這兩個東西的相似性,是不是高到在光學上有意義的程度。二零一二年出版的一篇論文對這個問題提出質疑[7],因為作者發現笛卡爾的插圖畫錯了!笛卡爾插圖中的非球面鏡片,底端有個尖角,不過如果你照著笛卡爾文字的指示做圖,就會發現正確的解答應該沒有那個尖角才對[8] 。Dalmanitina socialis 的透鏡下端有個小尖角,因此跟笛卡爾設計的透鏡其實有重要的不同。論文的作者猜測它跟球面像差無關。它的功能可能比較類似於我們用的雙焦眼鏡(bifocals):它的兩個焦點,可以降低方解石透鏡缺乏變焦功能所帶來的問題。創造論者愛講的「完美三葉蟲眼睛」,至少在 Dalmanitina socialis 這個例子上不能成立[9]。
這篇文章的標題叫「笛卡爾與三葉蟲」,你現在知道這兩個主題的關聯性,其實相當薄弱,可能只是個巧合罷了。不過笛卡爾在光學上的洞見,的確是在視覺科學上,有重要的影響。我們繞了這麼大一個圈子,多多少少還是值得的。
探查科學的歷史,有一種方法是追問科學理論是在什麼文化與思想背景下形成的。另一種方法是試著親自動腦動手,追隨前人的思路。笛卡爾與惠更斯兩人都是難得的天才,是我們一般人難以相比的。不過隨著知識的進展,以及教育科技的普及化,今日的我們只要善用笛卡爾推導出來的折射公式,要獨立推導出笛卡爾與惠更的鏡片公式,完全不費吹灰之力。我只花了一個下午的時間,靠著數學軟體 Mathematica 的幫忙,就得到了笛卡爾思考多年才得到的結果。有趣的地方是三度空間印表機在這幾年已經進步到了可以印製光學元件的程度。也許幾年之後,我們只要下一個指令,就可以實體擁有這些鏡片,到時所有的人都可以輕易廉價的實驗各種各種光學元件。也許這是笛卡爾在《折光學》裡構想的機器,最終極的實踐吧。
註釋:
- [1] 也就是所謂的「司乃耳定律」(Snell’s Law)。笛卡爾並不是第一個推導出這個定律的人,不過這裡他用跟前人不同的方法得到同樣的結論。
- [2]小說《玫瑰的名字》的讀者也許記得主角威廉,是十四世紀的僧人,就帶著一副眼鏡。
- [3] 例如說牛頓發現「色差」(chromatic aberration),也會影響成像的品質。色差造成的問題不能用笛卡爾的光學解決。
- [4] Dawkins, R. (1986) The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe without Design.
- [5] 最新的科技甚至讓科學家重建三葉蟲眼睛裡面感光神經的結構,三葉蟲因此是我們能研究最古老的視覺神經系統。見 Schoenemann, B. & Clarkson, E. N. K. (2013) Discovery of some 400 million year-old sensory structures in the compound eyes of trilobites. Scientific Reports 3, e1429。
- [6] 光學理論要等到牛頓的時候才開始成熟。笛卡爾的光學基礎其實非常的原始。因為他沒有考慮到色差等因素,他的鏡片嚴格說起來並不完美。不過三葉蟲的水底視覺,色差的問題並不嚴重,在這裡可以忽略。
- [7] Egri, A. & Horváth, G. (2012) Possible optical functions of the central core in lenses of trilobite eyes: spherically corrected monofocality or bifocality. J. Opt. Soc. Am. A 29, 1965.
- [8] 笛卡爾在《折光學》裡也有一張插圖描述非球面透鏡,這張插畫就沒有那個尖角。可見笛卡爾只是在準備《幾何學》插圖時,犯了一個小錯誤。我跟 Horváth 教授通過信,他說這個錯誤的確是在幾百年之內沒有人注意到,一直要等他用數學方法模擬三葉蟲的眼睛結構時才無意發現。
- [9] Crozonaspis 三葉蟲透鏡跟惠更斯透鏡的相似性,因為有比較直接的實驗證據,至今仍然被科學界認為是有對抗球面像差的功能。
參考資料:
- Ribe, N.M. (1997) Cartesian optics and the mastery of nature. Isis 88, 42–61.
- Burnett, D.G. (2005) Descartes and the hyperbolic quest: lens making machines and their significance in the seventeenth century. American Philosophical Society.
本文轉載自作職業科學家的業餘科學者。
The post 笛卡爾與三葉蟲有什麼關係? appeared first on PanSci 泛科學.